Quadratische Gleichungen und ihre Lösungen lassen sich sehr schön geometrisch veranschaulichen – eine Möglichkeit, die auch bei anderen Gleichungen hilfreich ist.
Die Lösungen der Gleichung
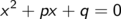
entsprechen den Nullstellen der quadratischen Funktion
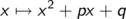
also den x-Koordinaten der Schnittpunkte des Graphens der Funktion (einer Parabel) mit der x-Achse.
Mit diesem geometrischen Blick auf quadratische Gleichungen sehen wir ohne Rechnung, allein durch Skizzieren einer Parabel, dass eine quadratische Gleichung keine, eine oder zwei reeelle Lösungen haben muss.
Um den Zusammenhang zur pq–Formel besser zu erkennen, malen wir die Parabeln für die drei Fälle einmal sorgfätig auf.
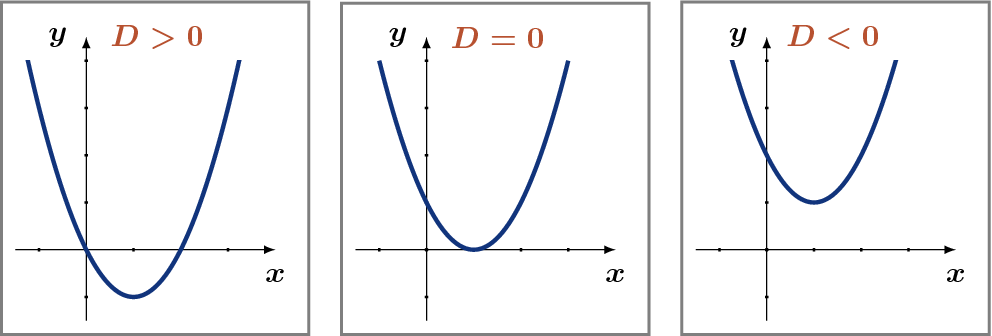
Bemerkung: Den Scheitelpunkt (–p/2, –D) der Parabel, das Minimum der Funktion, berechnet man als Nullstelle der ersten Ableitung oder mit Hilfe der quadratischen Ergänzung.
Überlegen Sie sich durch Skizzieren des Graphens der Funktion
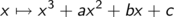
dass eine kubische Gleichung immer mindestens eine reelle Lösungen haben muss.
Überlegen Sie sich, wie der Graph für sehr große und sehr kleine Werte von x verläuft.
Für betragsmäßig große Werte dominiert der Term mit der höchsten Potenz.
Der Graph kann also eine, zwei oder drei Schnittpunkte mit der x–Achse haben.
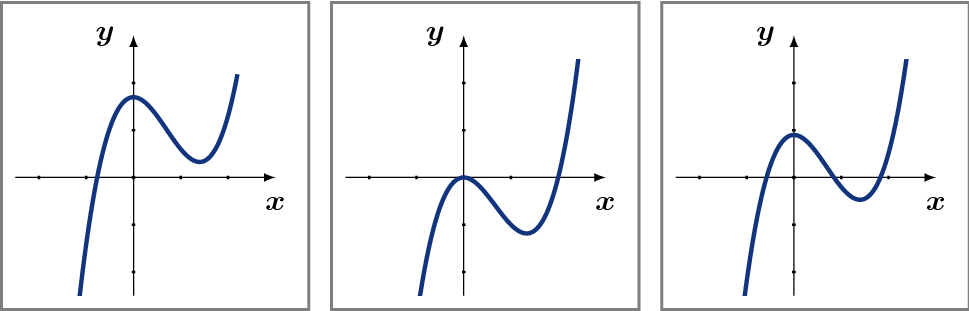
Eine kubische Gleichung kann demzufolge eine, zwei oder drei reelle Lösungen haben.
Soweit macht es noch Spass. Die – der pq-Formel entsprechende – Formel zur Berechnung der Lösungen ist aber in der Handhabung, nicht zu reden von der Herleitung, eher sperrig. (So werden reelle Lösungen als Differenz komplexer Zahlen berechnet.)