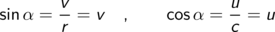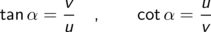
Die geometrische Definition der Winkelfunktionen, auch trigonometrische Funktionen genannt, erfolgt für spitze Winkel (Winkel kleiner 90 Grad) über die Längenverhältnisse der Seiten eines rechtwinkligen Dreiecks.
So ist der Sinus eines Winkels definiert als das Verhältnis der Länge der dem Winkel gegenüberliegenden Kathete (der Gegenkathete) zur Länge der Hypotenuse (der Seite, die dem rechten Winkel gegenüberliegt).
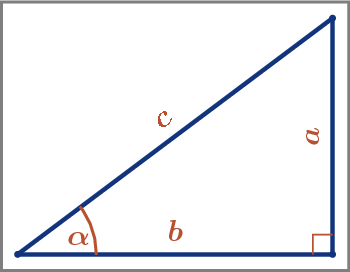
Zusammengefasst für alle vier Winkelfunktionen mit den aus dem Bild ersichtlichen Bezeichnungen für die Winkel und Seiten im rechtwinkligen Dreieck
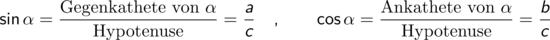

Um die Winkelfunktionen auch zur Beschreibung von Drehungen und Schwingungen nutzen zu können, müssen wir ihre Definition auf beliebige Winkel (127°, 359°, –40° …) ausweiten. Im Bereich der spitzen Winkel muss die neue Definition natürlich mit der alten übereinstimmen: das ist mit ausweiten gemeint.
Wichtiger als die Einzelheiten der erweiterten Definition ist, was hinten raus kommt: Die Kurvenbilder (Funktionsgraphen) von Sinus und Kosinus sollten Sie Bedarf skizzieren können.
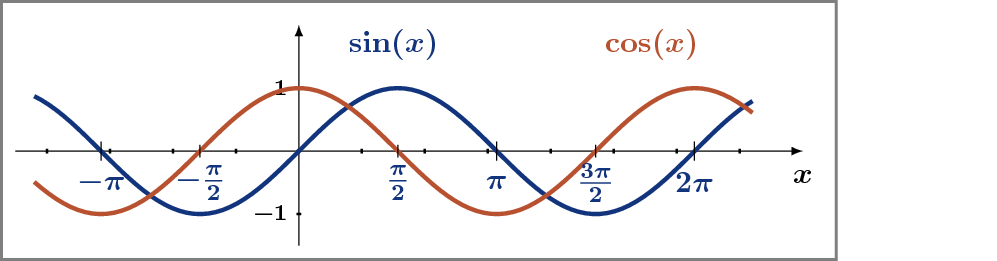
Wie üblich haben wir in der Abbildung die Winkel im Bogenmaß und nicht im Gradmaß angegeben. Das Maß 2 Pi entspricht also dem vollen Winkel.
Mit Mut zur großen Lücke die allerwichtigsten Eigenschaften, wobei Sie die Periodizität, die Symmetrie und die Verschiebung zwischen Sinus und Kosinus direkt an den Kurvenbildern ablesen können


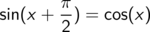
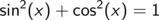

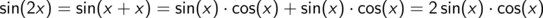
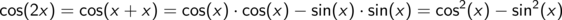
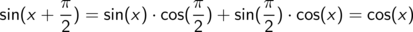
Damit niemand das Gefühl hat, ihm sei Wesentliches vorenthalten worden, als Nachtrag die Definition der Winkelfunktionen am Einheitskreis.
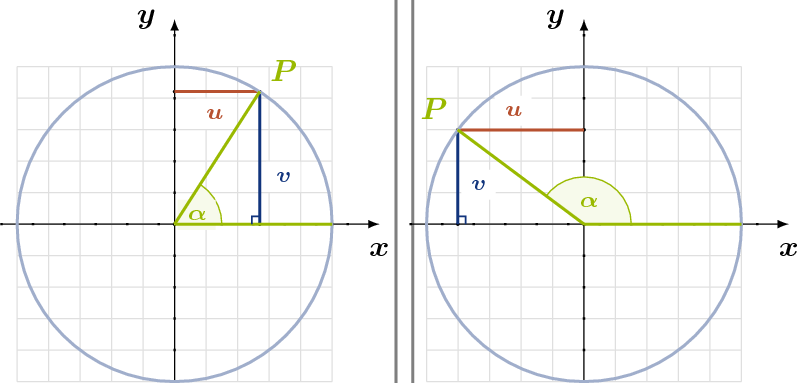
Wir wählen ein handelsübliches (x,y)-Koordinatensystem und legen in dessen Ursprung einen Kreis mit Radius r = 1. Dann betrachten wir den Winkel zwischen der positiven x-Achse als erstem Schenkel und einem beweglichen zweiten Schenkel. Der Winkel ist in dem Sinne orientiert, dass er ein positives Vorzeichen erhält, wenn wir den zweiten, beweglichen Schenkel gegen den Uhrzeigersinn drehen. Mit Hilfe der kartesischen Koordinaten (u, v) des Schnittpunktes P des beweglichen Schenkels mit dem Kreis definieren wir