Kehren wir noch einmal zum Anfang und damit zum Konzept der Ableitung in einem Punkt zurück.
Eine Funktion ist in einem Punkt differenzierbar, wenn man sie in der Umgebung dieses Punktes durch eine lineare Abbildung gut approximieren kann.
Als nächstes folgte die (bereits aus der Schule) bekannte Definition der Ableitung als Grenzwert der Differenzenquotienten.
Eine Funktion f heißt an einer Stelle x0 ihres Definitionsbereichs differenzierbar, wenn der Grenzwert
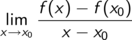
existiert.
Diesen Grenzwert nennt man die Ableitung der Funktion f an der Stelle x0 und bezeichnet ihn als f’(x0).
Auf den ersten Blick sieht man dieser Definition nicht an, was sie mit lokaler Linearisierung zu tun hat. Deshalb riskieren wir zum Abschluss einen zweiten Blick.
Wir wählen eine Stelle x0 und zerlegen eine an dieser Stelle differenzierbare Funktion f in einen in (x - x0) linearen Anteil und den Rest
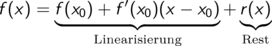
Wegen der Differenzierbarkeit verschwindet die Abweichung vom linearen Verlauf, der Rest, bei Annäherung an x0.
Und dies sogar schneller als x - x0, also selbst nach Division durch x - x0
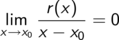
Der Rest enthält also Terme der Art
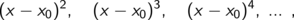
sogenannte Terme höherer Ordnung in (x - x0).
Zusammengefasst: Die Differenzierbarkeit in x0 stellt sicher, dass im Limes die Abweichung vom Linearen keine Rolle spielt, ignoriert werden kann.
Diese Eigenschaft charakterisiert die Differenzierbarkeit sogar.
Eine Funktion f ist an der Stelle x0 differenzierbar, wenn es eine lineare Abbildung L gibt, so dass gilt:
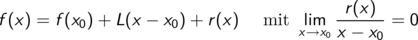
In dieser Forn ist die Differenzierbarkeit direkt auf Funktionen mehrerer Variabler oder Funktionen einer komplexen Variablen verallgemeinerbar.